javascript中解析四则运算表达式的算法和示例_javascript技巧

一、熟悉概念

中缀表示法（或中缀记法）是一个通用的算术或逻辑公式表示方法， 操作符是以中缀形式处于操作数的中间（例：3 + 4）。也就是我们最常用的算术表达式，中缀表达式对于人类来说比较容易理解，但是不易于计算机解析。

逆波兰表示法（Reverse Polish notation，RPN，或逆波兰记法），是一种是由波兰数学家扬·武卡谢维奇1920年引入的数学表达式方式，在逆波兰记法中，所有操作符置于操作数的后面，因此也被称为后缀表示法。逆波兰记法不需要括号来标识操作符的优先级。逆波兰表示法容易使用堆栈结构对表达式进行解析并计算，所以，这里我们解析四则元素表达式，是先从中缀表达式，转换为逆波兰表达式。然后再计算值。

二、转换流程

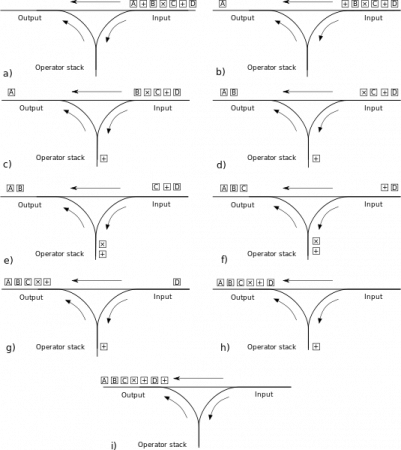
中缀表达式转换为后缀表达式（调度场算法）

1.输入队列弹出一个记号
2.如果记号为数字，添加到输出队列中
3.如果是一个操作符（+-*/）则比较它与输出堆栈中栈顶的操作符，如果优先级小于或等于栈顶的操作符，那么将栈顶的操作符弹出并加入输出队列（循环，直到上述条件不满足），最后将本次的操作符压入堆栈。
4.如果是一个左括号，压入堆栈
5.如果是一个右括号，从栈中不断的弹出操作符，并加入输出队列，知道栈顶的元素为左括号。弹出左括号，不加入输出队列。如果没有发现左括号，说明原来的表达式中括号不对称，有错误。
6.如果输入队列为空，而栈中尚有操作符时，如果栈顶的操作符为左括号，则说明原表达式有不匹配的括号。将栈中的操作符逐个弹出，加入输出队列。
7.完成

三、转换代码实现

四、逆波兰表达式求值

1.从输入队列中弹出一个记号
2.如果是操作数，加入输出堆栈
3.如果是一个操作符，从输出堆栈中弹出两个操作数并进行计算，并将计算得到的值压入输出堆栈。
4.循环操作，如果输入队列为空，且输出堆栈只有一个数则这个数为结果，否则是出现了多余的操作数。

五、计算代码

六、结语

逆波兰表示法，在初次接触的时候感觉不太习惯，但是熟悉之后，会发现，其实思路特别简单，不像中缀表示法，还有各种优先级啊，还有小括号之类的，逻辑特别麻烦，还是逆波兰表示法比较简洁，完全不用考虑优先级，也没用小括号，中括号还有大括号搅局。